Beaver: This is a tool for computing the over-approximate reach set of the parameterized linear dynamical system given by,

ẋ(t) = Ax(t), x(0) ∈ X₀ ⊆ ⁿ, A ∈ Ω, t ∈ [0,T]                                (1) within desired error tolerance ε > 0, where X₀ and Ω ⊆ ^n×n, are compact polyhedral sets, A is a n×n dimensional matrix and [0,T] is the time domain of interest. This tool computes the over approximate reach set in the form of SMT expressions in SMT Lib format. We use Z3-SMT solver for safety verification of system (1) from the given unsafe region.

Reach set: The state of the System (1) starting from an initial state x(0) ∈ X₀ for a matrix A ∈ Ω at time t is given by the state transition function defined as:

Φ(x(0), A, t) = e^At x(0) The reach set of the System (1) is given by, Reach_Φ(X(0), Ω, [0,T]) = {Φ(x(0), A, t) | x(0) ∈ X₀, A ∈ Ω, t ∈ [0,T]}

Verification: This tool is useful for safety verification of the reach set of the parameterized linear dynamical system from the given unsafe region. It is shown in below figure.

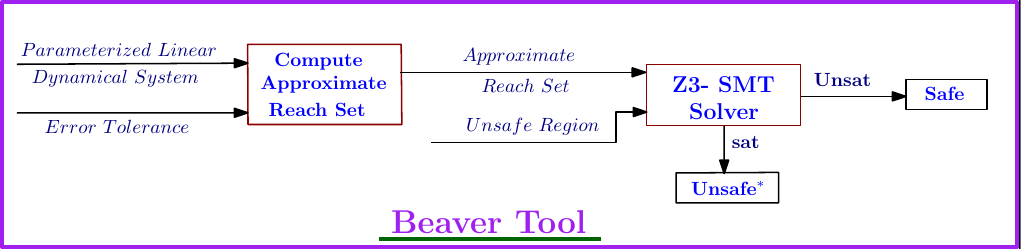In the above figure, if the Z3-SMT solver gives the output unsat, the Reach_Φ (X(0), Ω, [0,T]) does not intersect with unsafe region, i.e. it is safe and if the output is sat, the ε-ball of reach set B_ε (Reach_Φ(X(0), Ω, [0,T])) intersects with the unsafe region i.e. it is Unsafe^*. The Unsafe^* guarantees that the reach set of the parameterized linear dynamical system is unsafe within the error tolerance ε > 0.